今天,东南教育网小编为大家带来了2015年高考理科数学试题预测卷,希望能帮助到大家,一起来看看吧!


参考公式:锥体的体积公式 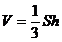 ,其中
,其中 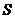 是锥体的底面积,
是锥体的底面积, 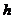 是锥体的高.
是锥体的高.
如果事件 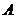 、
、 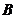 互斥,那么
互斥,那么 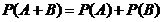 .
.
用最小二乘法求线性回归方程系数公式, 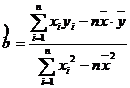 ,
, 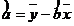 .
.
一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、 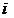 是虚数单位,
是虚数单位, 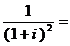 ( )
( )
A. 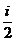 B.
B. 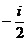 C.
C.  D.
D. 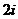
2、函数 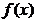 的定义域为实数集
的定义域为实数集 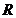 ,“
,“ 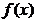 是奇函数”是“
是奇函数”是“ 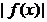 是偶函数”的( )
是偶函数”的( )
A.充分非必要条件 B.必要非充分条件
C.非充分非必要条件 D.充要条件
3、 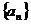 是等差数列,
是等差数列, 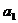 与
与 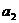 的等差中项为1,
的等差中项为1, 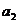 与
与 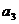 的等差中项为2,则公差
的等差中项为2,则公差 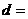 ( )
( )
A. 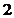 B.
B. 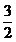 C.
C.  D.
D. 
4、函数 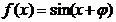 在区间
在区间 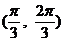 上单调递增,常数
上单调递增,常数 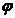 的值可能是( )
的值可能是( )
A. 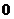 B.
B. 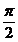 C.
C. 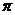 D.
D. 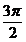
5、双曲线  :
: 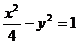 的两条渐近线夹角(锐角)为
的两条渐近线夹角(锐角)为 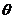 ,则
,则 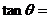 ( )
( )
A. 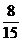 B.
B. 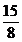 C.
C. 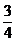 D.
D. 
6、一个四面体如图1,若该四面体的正视图(主视图)、侧视图(左视图)和俯视图都是直角边长为1
 的等腰直角三角形,则它的体积
的等腰直角三角形,则它的体积 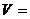 ( )
( )
A.  B.
B.  C.
C. 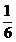 D.
D. 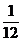
7、 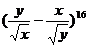 的二项展开式17个项中,整式的个数是( )
的二项展开式17个项中,整式的个数是( )
A.  B.
B. 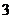 C.
C. 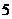 D.
D. 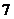
8、设 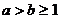 ,集合
,集合 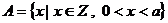 ,
, 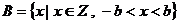 ,记“从集合
,记“从集合 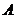 中任取一个元素
中任取一个元素 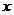 ,
, 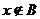 ”为事件
”为事件 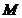 ,“从集合
,“从集合 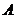 中任取一个元素
中任取一个元素 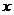 ,
, 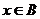 ”为事件
”为事件 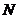 .给定下列三个命题:
.给定下列三个命题:
①当 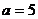 ,
, 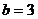 时,
时, 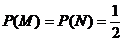 ;
;
②若 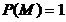 ,则
,则 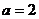 ,
, 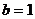 ;
;
③ 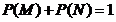 恒成立.
恒成立.
其中,为真命题的是( )
A.①② B.①③ C.②③ D.①②③
二、填空题:本大题共7小题,考生作答4小题,每小题5分,满分30分.
(一)必做题(9~13题)
9.不等式  的解集为 .
的解集为 .
10.已知抛物线  :
: 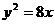 的焦点为
的焦点为 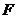 ,
, 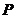 是
是  上一点,若
上一点,若 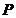 在第一象限,
在第一象限, 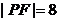 ,
,
则点 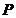 的坐标为 .
的坐标为 .
11.若变量 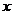 、
、 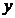 满足约束条件
满足约束条件 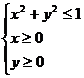 ,则
,则 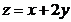 的最大值
的最大值 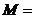 .
.
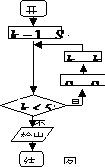
12.运行如图2所示的程序框图,输出的结果 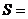 .
.
13.已知 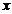 与
与 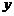 之间的几组数据如下表:
之间的几组数据如下表:
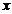 | 3 | 4 | 5 | 6 |
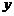 | 2.5 | 3 | 4 | 4.5 |
假设根据上表数据所得线性回归方程为 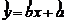 ,根据中间两组数据(4,3)和(5,4)求得的直线方程为
,根据中间两组数据(4,3)和(5,4)求得的直线方程为 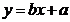 ,则
,则  ,
,  .(填“
.(填“ 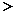 ”或“
”或“ 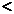 ”)
”)
(二)选做题(14、15题,考生只能从中选做一题)
14.(坐标系与参数方程选做题)在极坐标系中,曲线 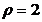 上到直线
上到直线 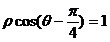 的距离为1的点的个数是 .
的距离为1的点的个数是 .
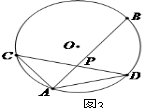 15.(几何证明选讲选做题)如图3,圆
15.(几何证明选讲选做题)如图3,圆 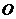 的弦
的弦 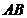 、
、 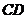 相交于点
相交于点 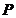 ,若
,若 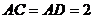 ,
, 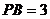 ,则
,则 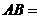 .
.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(本小题满分12分)
已知 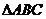 顶点的直角坐标分别是
顶点的直角坐标分别是 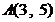 、
、 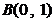 、
、 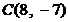 .
.
⑴求 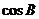 的值;
的值;
⑵若 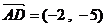 ,证明:
,证明: 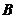 、
、 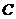 、
、 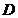 三点共线.
三点共线.
17.(本小题满分13分)
某树苗培育基地为了解其基地内榕树树苗的长势情况,随机抽取了100株树苗,分别测出它们的高度(单位: 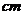 ),并将所得数据分组,画出频率分布表如下:
),并将所得数据分组,画出频率分布表如下:
| 组距 | 频数 | 频率 |
| [100,102) | 17 | 0.17 |
| [102,104) | 18 | 0.18 |
| [104,106) | 24 | 0.24 |
| [106,108) | 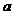 | 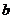 |
| [108,110) | 6 | 0.06 |
| [110,112) | 3 | 0.03 |
| 合计 | 100 | 1 |
⑴求上表中 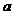 、
、 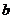 的值;
的值;
⑵估计该基地榕树树苗平均高度;
⑶基地从上述100株榕树苗中高度在[108,112)范围内的树苗中随机选出5株进行育种研究,其中在[110,112)内的有 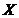 株,求
株,求 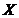 的分布列和期望.
的分布列和期望.
18.(本小题满分14分)
设数列 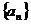 的前
的前 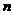 项和
项和 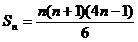 ,
, 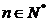 .
.
⑴求 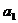 的值;
的值;
⑵求数列 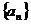 的通项公式;
的通项公式;
⑶证明:对一切正整数 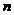 ,有
,有 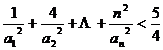 .
.
19.(本小题满分13分)
如图4,直四棱柱 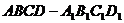 的底面是菱形,侧面是正方形,
的底面是菱形,侧面是正方形, 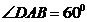 ,
, 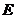 是棱
是棱 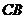 的延长线上一点,经过点
的延长线上一点,经过点 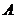 、
、 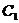 、
、 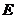 的平面交棱
的平面交棱 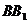 于点
于点 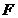 ,
, 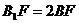 .
.
 ⑴求证:平面
⑴求证:平面 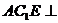 平面
平面 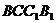 ;
;
⑵求二面角 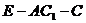 的平面角的余弦值.
的平面角的余弦值.
20.(本小题满分14分)
平面直角坐标系 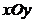 中,椭圆
中,椭圆  :
: 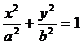 (
( 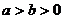 )的离心率为
)的离心率为  ,焦点为
,焦点为 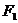 、
、 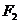 ,
,
直线 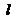 :
: 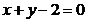 经过焦点
经过焦点 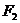 ,并与
,并与 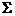 相交于
相交于 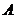 、
、 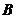 两点.
两点.
⑴求 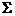 的方程;
的方程;
⑵在 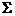 上是否存在
上是否存在 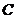 、
、 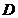 两点,满足
两点,满足 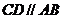 ,
, 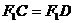 ?若存在,求直线
?若存在,求直线 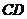 的方程;
的方程;
若不存在,说明理由.
21.(本小题满分14分)
设函数 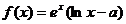 ,
, 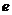 是自然对数的底数,
是自然对数的底数, 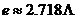 ,
, 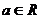 为常数.
为常数.
⑴若 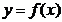 在
在 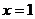 处的切线
处的切线 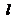 的斜率为
的斜率为 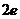 ,求
,求 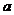 的值;
的值;
⑵在⑴的条件下,证明切线 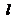 与曲线
与曲线 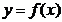 在区间
在区间 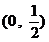 至少有1个公共点;
至少有1个公共点;
⑶若 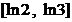 是
是 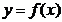 的一个单调区间,求
的一个单调区间,求 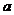 的取值范围.
的取值范围.
评分参考答案
一、选择题 BACD DCBB
二、填空题 ⒐ 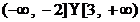 或
或 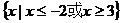 (每个区间2分,在此基础上正确用区间或集合表示1分;若混淆闭区间与开区间则扣该区间1分。)
(每个区间2分,在此基础上正确用区间或集合表示1分;若混淆闭区间与开区间则扣该区间1分。)
⒑ 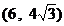 (若写成
(若写成 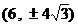 或
或 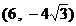 给3分,其他不给分)
给3分,其他不给分)
⒒ 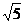 ⒓
⒓ 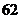 ⒔
⒔ 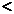 ,
, 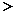 (若两空一对一错,给3分) ⒕
(若两空一对一错,给3分) ⒕ 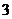 ⒖
⒖ 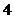
三、解答题
⒗⑴(方法一) 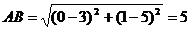 ,
, 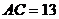 ,
, 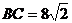 ……3分
……3分
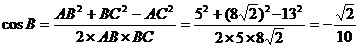 ……6分(公式2分)
……6分(公式2分)
(方法二) 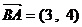 ,
, 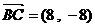 ……2分
……2分
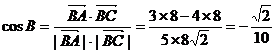 ……6分(公式2分)
……6分(公式2分)
⑵(方法一) 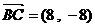 ,
, 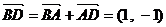 ……9分
……9分
∵ 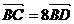 ,∴
,∴ 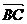 、
、 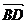 共线……11分
共线……11分
∵ 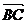 、
、 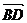 有共同的始点,∴
有共同的始点,∴ 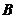 、
、 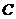 、
、 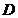 三点共线……12分
三点共线……12分
(方法二)经过 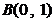 、
、 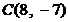 两点的直线
两点的直线 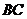 的方程为
的方程为
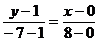 (即
(即 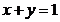 )……9分
)……9分
设 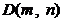 ,由
,由 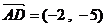 得
得 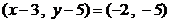 ……10分
……10分
解得 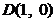 ……11分
……11分
∵ 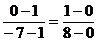 (或
(或 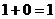 ),∴(
),∴( 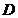 在
在 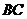 上)
上) 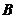 、
、 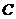 、
、 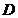 三点共线……12分
三点共线……12分
⒘⑴ 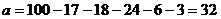 ,
, 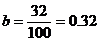 ……2分
……2分
⑵估计该基地榕树树苗平均高度为
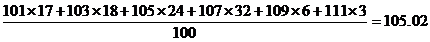 (
(  )……6分
)……6分
(列式2分,求值1分,文字说明与单位完整1分。)
⑶由频率分布表知树苗高度在[108,112)范围内的有9株,在[110,112)范围内的有3株,因此 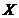 的所有可能取值为0,1,2,3……7分
的所有可能取值为0,1,2,3……7分
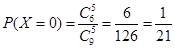 ,
, 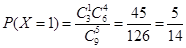 ,
,
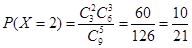 ,
, 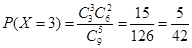
……11分
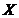 | 0 | 1 | 2 | 3 |
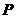 | 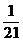 | 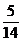 | 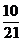 | 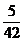 |
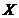 的分布列为
的分布列为
……12分
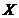 的期望为
的期望为 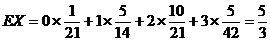 ……13分(列式正确1分)
……13分(列式正确1分)
⒙⑴ 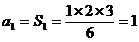 ……1分
……1分
⑵ 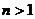 时,
时, 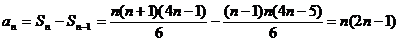
……4分(上式每个等号1分)
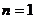 时,
时,  ,所以
,所以 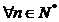 ,
, 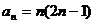 ……5分
……5分
⑶由⑵知, 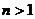 时,
时, 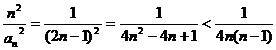 ……7分
……7分
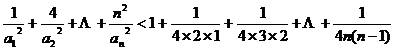 ……9分
……9分
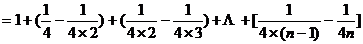 ……11分
……11分
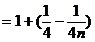 ……12分,
……12分, 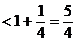 ……13分
……13分
∵ 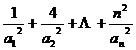 单调递增,∴
单调递增,∴ 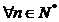 ,
, 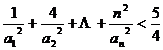 ……14分
……14分
⒚⑴设四棱柱 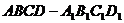 的棱长为
的棱长为 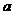
∵ 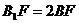 ,
,  ∽
∽ 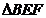 ,∴
,∴ 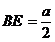 ……1分
……1分
由 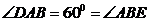 ,
, 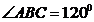 ,得
,得 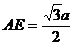 ,
, 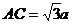 ……2分
……2分
∵ 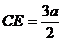 ,∴
,∴ 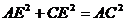 ,
, 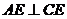 ……3分
……3分
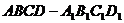 是直四棱柱,
是直四棱柱, 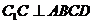 ,又
,又 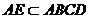 ,∴
,∴ 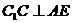 ,∵
,∵ 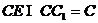 ,∴
,∴ 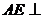 平面
平面 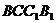 ……4分
……4分
∵ 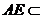 平面
平面 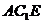 ,∴平面
,∴平面 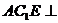 平面
平面 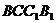 ……5分
……5分
⑵(方法一)过 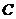 作
作 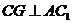 于
于 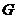 ,
, 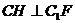 于
于 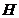 ,连接
,连接 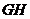 ……6分
……6分
由平面 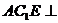 平面
平面 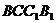 ,平面
,平面 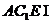 平面
平面 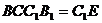 ,
,
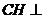 平面
平面 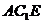 ……7分
……7分
∴ 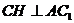 ,又
,又 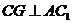 ,
, 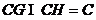 ,∴
,∴ 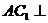 平面
平面 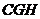 ,
, 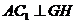 ,
, 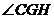 是二面角
是二面角 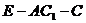 的平面角……9分
的平面角……9分
在 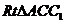 中,
中, 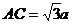 ,
, 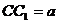 ,
, 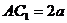 ,
, 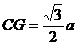 ,在
,在 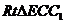 中,
中, 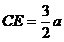 ,
, 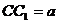 ,
, 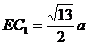 ,
, 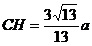 (
( 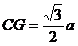 、
、 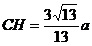 求得任何一个给2分,两个全对给3分)……12分
求得任何一个给2分,两个全对给3分)……12分
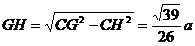 ,
, 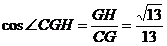 ……13分
……13分
(方法二)以 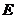 为原点,
为原点, 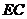 、
、 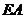 所在直线为
所在直线为 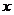 轴、
轴、 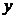 轴,平行于
轴,平行于 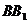 的直线
的直线 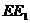 为
为 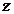 轴建立空间直角坐标系……6分,则
轴建立空间直角坐标系……6分,则
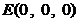 ,
, 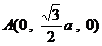 ,
, 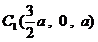 ……7分
……7分
设平面 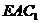 的一个法向量为
的一个法向量为 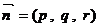 ,则
,则 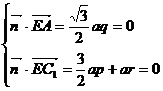 ……9分,即
……9分,即 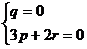 ,不妨取
,不妨取 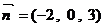 ……10分,由⑴知
……10分,由⑴知 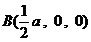 ,
, 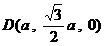 ……11分,平面
……11分,平面 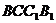 的一个法向量为
的一个法向量为 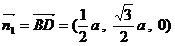
……12分,二面角 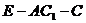 的平面角的余弦值
的平面角的余弦值 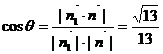 ……13分
……13分
⒛⑴依题意 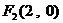 ,
, 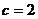 ……2分,由
……2分,由 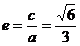 得
得 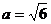 ……3分
……3分
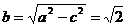 ,椭圆
,椭圆 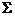 的方程为
的方程为 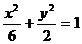 ……4分
……4分
⑵(方法一)若存在满足条件的直线 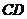 ,∵
,∵ 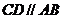 ,∴
,∴ 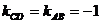 ,设直线
,设直线 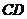 的方程为
的方程为 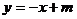 ……5分
……5分
由 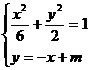 ……6分,得
……6分,得 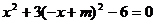 ……7分
……7分
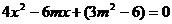 ,
, 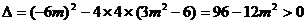 (*)
(*)
……8分
设 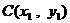 ,
, 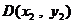 ,则
,则 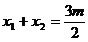 ,
, 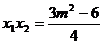 ……9分
……9分
由已知 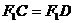 ,若线段
,若线段 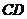 的中点为
的中点为 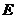 ,则
,则 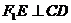 ,
, 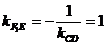 ……10分
……10分
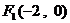 ,
, 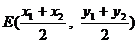 即
即 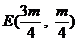 ……11分
……11分
由 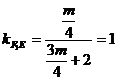 ……12分,解得
……12分,解得 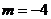 ……13分
……13分
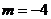 时,
时, 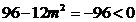 ,与(*)矛盾,∴不存在满足条件的直线
,与(*)矛盾,∴不存在满足条件的直线 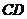
……14分
(方法二)假设存在 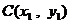 ,
, 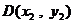 ,线段
,线段 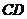 的中点为
的中点为 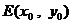 ,则
,则 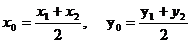 ,
, 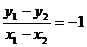 ……5分
……5分
由 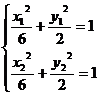 两式相减得:
两式相减得: 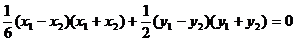
……7分,代入、化简得: 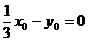 ①……8分
①……8分
由已知 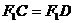 ,则
,则 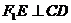 ,
, 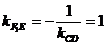 ……9分
……9分
由 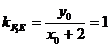 得,
得, 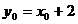 ②……10分
②……10分
由①②解得 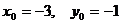 ,即
,即 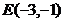 ……11分
……11分
直线CD的方程为: 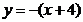 ……12分
……12分
联立 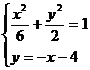 得
得 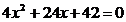 ……13分
……13分
∵ 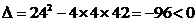 ,方程(组)无解,∴不存在满足条件的直线
,方程(组)无解,∴不存在满足条件的直线 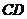
……14分
21.⑴ 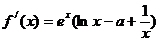 ……1分
……1分
依题意, 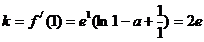 ,解得
,解得 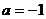 ……2分
……2分
⑵由⑴ 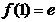 ,直线
,直线 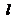 的方程为
的方程为 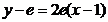 ,即
,即 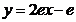 ……3分
……3分
作 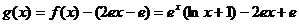 ,
,
则 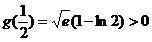 ……4分,
……4分, 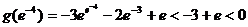 ……5分(用其他适当的数替代
……5分(用其他适当的数替代 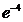 亦可)
亦可)
因为 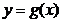 在
在 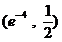 上是连续不断的曲线,
上是连续不断的曲线, 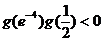 ,
, 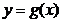 在
在 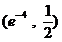 内有零点,
内有零点, 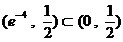 ,从而切线
,从而切线 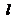 与曲线
与曲线 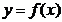 在区间
在区间 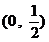 至少有1个公共点……6分
至少有1个公共点……6分
⑶ 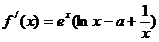 ,
, 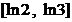 是
是 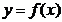 的一个单调区间当且仅当
的一个单调区间当且仅当 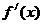 在
在 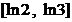 上恒大于等于零,或恒小于等于零,由
上恒大于等于零,或恒小于等于零,由 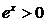 ,作
,作 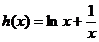
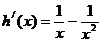 ,由
,由 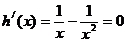 得
得 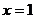 ……7分
……7分
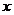 | 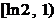 |  | 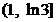 |
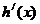 | - | 0 | + |
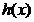 | ↘ | 最小值 | ↗ |
……9分
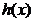 在
在 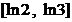 上的最小值为
上的最小值为 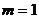 ,所以,当且仅当
,所以,当且仅当 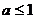 时,
时, 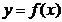 在
在 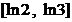 上单调递增……11分
上单调递增……11分
下面比较 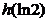 与
与 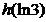 的大小
的大小
(方法一)由 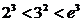 ,
, 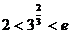 ,
, 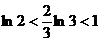 以及
以及 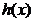 在
在 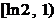 上单调递减得
上单调递减得 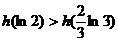 ……12分
……12分
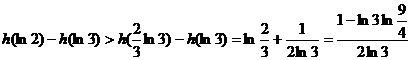 ……13分
……13分
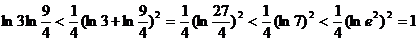 ,
,
∴ 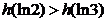 ,当且仅当
,当且仅当 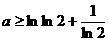 时,
时, 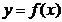 在
在 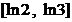 上单调递减,综上所述,
上单调递减,综上所述, 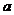 的取值范围为
的取值范围为 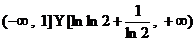 ……14分
……14分
(方法二)由 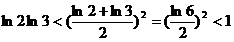 ,
, 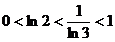 ,以及
,以及 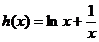 的单调性知,
的单调性知, 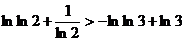 ……12分
……12分
由 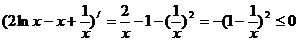 知,
知, 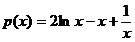 单调递减……13分
单调递减……13分
由 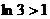 得
得 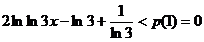 ,
, 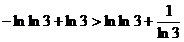 ,
, 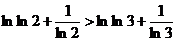 ,∴
,∴ 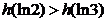 ,当且仅当
,当且仅当 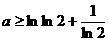 时,
时, 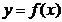 在
在 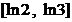 上单调递减,综上所述,
上单调递减,综上所述, 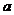 的取值范围为
的取值范围为 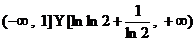 ……14分
……14分
(“单调递增……11分”以下,若直接写 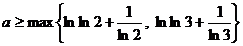 ,再给1分)
,再给1分)



以上就是东南教育网整理的2015年高考理科数学试题预测卷相关内容,想要了解更多信息,敬请查阅东南教育网。
本文标题:2015年高考理科数学试题预测卷
wap地址: https://m.dngk.com/newsdetail/76996.html